Linear Algebra
CholeskyGetL
Returns the lower triangular factor L of a Cholesky decomposition, such that L*L'=A.
CholeskySolve
Returns the solution x of the problem Ax = b for x using Cholesky decomposition. x can be a matrix or vector.
condition
Returns the condition number of the matrix: max(S)/min(S).
count
Returns the number of cells in a tensor
countRange
Returns the number of values within a given range.
-
x: is the container for which you want to count the values.
-
min: is the lower boundary of the range. The lower boundary is not included in the range.
-
max: is the upper boundary of the range. The upper boundary is included in the range.
covarianceMatrix
Calculates the matrix product of the given matrices.
determinant
Returns the determinant of the matrix.
EigenproblemGetD
Returns matrix D of A = V*D*V'.
Eigenvalues
Returns a vector listing the complex eigenvalues of the matrix or a single eigenvalue.
-
X: The matrix to be tested.
-
complex: true: return complex part of the eigenvalues (optional)
-
index: Index (0 : all, 1 : greatest, 2...)
-
ahp: true: calculate each group separately
Eigenvectors
Returns a matrix listing the eigenvectors of the given matrix.as columns (in dimension 1) and the values in dimension 0.
inverse
Returns the inverse of the matrix. The matrix must be invertible, otherwise the result is undefined.
isFullRank
Returns true if the matrix is of full rank
isNonsingular
Returns true if the matrix is nonsingular
isSPD
Returns true if the matrix is symmetric positive definite.
linearMapping
Performs a mapping from a source vector to another vector space using either the weighted sum method or the proportional score method.
Result: The linearMapping function maps a score for one dimension of a matrix to a score on the other dimension of a matrix using either the weighted sum method or the proportional score method.
-
matrix: is the matrix describing the linear transformation.
-
x: is the vector you want to map.
-
sign: sets a filter for the matrix relations: all, pos(itive only), neg(ative only)
-
total: total sum for normalization. Use 0 in order to skip normalization.
-
grouphandling: defines how to handle parent items: shallow (leafs only), sums (accumulate hierarchically), levels (calculate system level and paramater level separately).
-
method: wsm (weighted sum method) or prop (proportional score method)
-
causeslevel: is the details level for the causes. Set to 0 in order to use the matrix default.
-
effectslevel: is the details level for the effects. Set to 0 in order to use the matrix default.
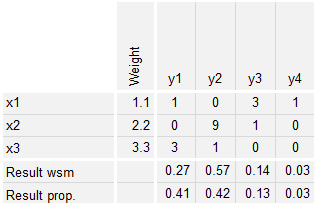
Calculation using weighted sum method:
- for each row in the matrix multiply all values by the corresponding value in the input vector
- calculate the sum of all columns in the matrix
- optionally normalize the sum to a given total, e.g. 1.0: sum up all values in the output vector, then divide each value of the output vector by this sum.
Calculation using proportional score method:
- calculate the sum of all columns in the matrix
- for each row in the matrix multiply all values by the corresponding value in the input vector
- divide all values in the matrix by the factor calculated in step 1.
- calculate the sum of all columns in the matrix
- optionally normalize the sum to a given total, e.g. 1.0: sum up all values in the output vector, then divide each value of the output vector by this sum.
LUGetL
Returns matrix L of the LU decomposition of the given matrix.
LUGetPivot
Returns the Pivot vector of the LU decomposition of the given matrix.
LUGetU
Returns matrix U of the LU decomposition of the given matrix.
LUSolve
Returns solution x of the problem Ax = b for x using LU decomposition.
-
A: Matrix A of the problem Ax = b. A can be an m-by-n matrix with m<>n.
-
b: Vector (or matrix) b of the problem Ax = b.
matrixProduct
Calculates the matrix product of the given matrices.
norm
Normalizes the numbers in a container to a given total.
-
x: is the container which contains the values you want to normalize.
-
total: is the sum you want to use for normalization, e.g. 100 if you want to express the values from container x in percent.
-
level: is the level of details to operate on
-
sumdim: specifies the dimension for the operation if the source is a multi-dimensional collection
-
: is the container which contains the values you want to normalize.
-
: is the sum you want to use for normalization, e.g. 100 if you want to express the values from container x in percent.
-
: is the level of details to operate on
-
: specifies the dimension for the operation if the source is a multi-dimensional collection
norm2
Returns the 2 norm (max(S)) of the matrix
nsum
Adds all negative numbers in a container.
percentage
Normalizes the numbers in a container to a total of 1.0.
-
x: is the container which contains the values you want to normalize.
-
level: is the level of details to operate on
-
sumdim: specifies the dimension for the operation if the source is a multi-dimensional collection
prod
Multiplies all the numbers in the given container and returns the product.
pseudoInverse
Returns the More-Penrose pseudoinverse of the matrix.
psum
Adds all positive numbers in a container.
QRGetHouseholder
Returns the Householder vectors from the QR decomposition of the given matrix.
QRGetQ
Returns matrix Q of the QR decomposition of the given matrix.
QRGetR
Returns matrix R of the QR decomposition of the given matrix.
QRSolve
Returns solution x of the problem Ax = b for x using QR decomposition.
rank
Returns the rank of the matrix.
sum
Adds all the numbers in a container.
SVDGetS
Returns matrix S of the SVD decomposition of the given matrix.
SVDGetSV
Returns a vector of singular values. Values are ordered from large to small.
SVDGetU
Returns matrix U of the SVD decomposition of the given matrix.
SVDGetV
Returns matrix V of the SVD decomposition of the given matrix.
SVDSolve
Solves the problem Ax = b for x using singular value decomposition
transposed
Returns the transposed of the given auto matrix.
Feedback
Did you find what you needed?
If you have any further questions or suggestions to improve this page, please let us know: